QN-Mixer: A Quasi-Newton MLP-Mixer Model for Sparse-View CT Reconstruction
Ishak Ayad (1,2), Nicolas Larue (1), Maï K. Nguyen (1)
(1) ETIS (UMR 8051), CY Cergy Paris University, ENSEA, CNRS, France
(2) AGM (UMR 8088), CY Cergy Paris University, CNRS, France

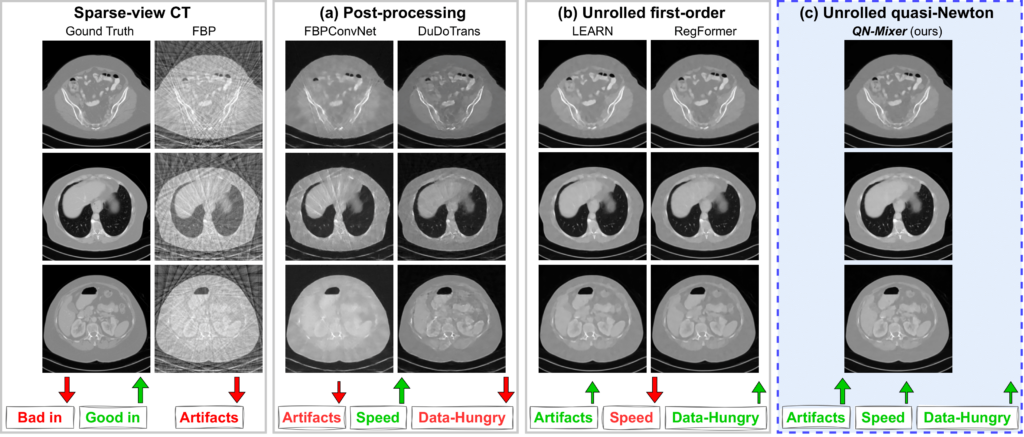
Inverse problems span across diverse fields. In medical contexts, computed tomography (CT) plays a crucial role in reconstructing a patient’s internal structure, presenting challenges due to artifacts caused by inherently ill-posed inverse problems. Previous research advanced image quality via post-processing and deep unrolling algorithms but faces challenges, such as extended convergence times with ultra-sparse data. Despite enhancements, resulting images often show significant artifacts, limiting their effectiveness for real-world diagnostic applications. We aim to explore deep second-order unrolling algorithms for solving imaging inverse problems, emphasizing their faster convergence and lower time complexity compared to common first-order methods like gradient descent. In this paper, we introduce QN-Mixer, an algorithm based on the quasi-Newton approach. We use learned parameters through the BFGS algorithm and introduce Incept-Mixer, an efficient neural architecture that serves as a non-local regularization term, capturing long-range dependencies within images. To address the computational demands typically associated with quasi-Newton algorithms that require full Hessian matrix computations, we present a memory-efficient alternative. Our approach intelligently downsamples gradient information, significantly reducing computational requirements while maintaining performance. The approach is validated through experiments on the sparse-view CT problem, involving various datasets and scanning protocols, and is compared with post-processing and deep unrolling state-of-the-art approaches. Our method outperforms existing approaches and achieves state-of-the-art performance in terms of SSIM and PSNR, all while reducing the number of unrolling iterations required.

More details: https://towzeur.github.io/QN-Mixer/